Did Drug Decriminalization Increase OD Deaths?

Two new studies disagree!

Let’s talk about the Basque Country.

The Basque Country is one of Spain’s “autonomous communities,” the highest level of sub-national division of the post-Franco Spanish republic. Located in northern Spain, it is home to the Basque people, a group of about 2.4 million who have a distinct culture, including a language, Basque, that is linguistically distinct from Spanish, French, and the languages of other nearby peoples. The Basque Country is historically quite wealthy, ranking first among the autonomous communities for median income. But it also has a bloody past. Between the late 1960s and 2011, separatists lead by the group Euskadi Ta Askatasuna (ETA) waged a deadly guerilla war with the aim of securing an independent Basque state.

At the outset of the ETA’s terrorism, the Basque country was the third richest region in Spain (out of 17); by the late 1990s, after 20 years of ETA bombings and almost 800 deaths, it dropped to sixth. This raises a question: To what extent did the Basque conflict cause the Basque Country’s economic decline? A naive way to answer this question would be to compare the Basque Country to Spain’s other autonomous communities. But doing so does not allow us to isolate the effects of ETA terrorism; what about other, unobserved differences between the Basque Country and the comparison communities?

One answer comes from Abadie and Gardeazabal 2003, which (lucky for us!) attacks this very question in a novel way. Specifically, the authors construct what they call a “synthetic control.” Specifically, what they do is collect data about the economic trajectory of all of the autonomous communities. They then algorithmically construct a weighted average of the non-Basque units designed to minimize the difference between it and the observed Basque Country’s economic data prior to the full-scale onset of the ETA’s terrorist campaign in 1975. The values after this point are then taken to be the counterfactual—the path that the Basque Country would have taken absent the ETA’s bombing campaign.

Source: Abadie and Gardeazabal 2003

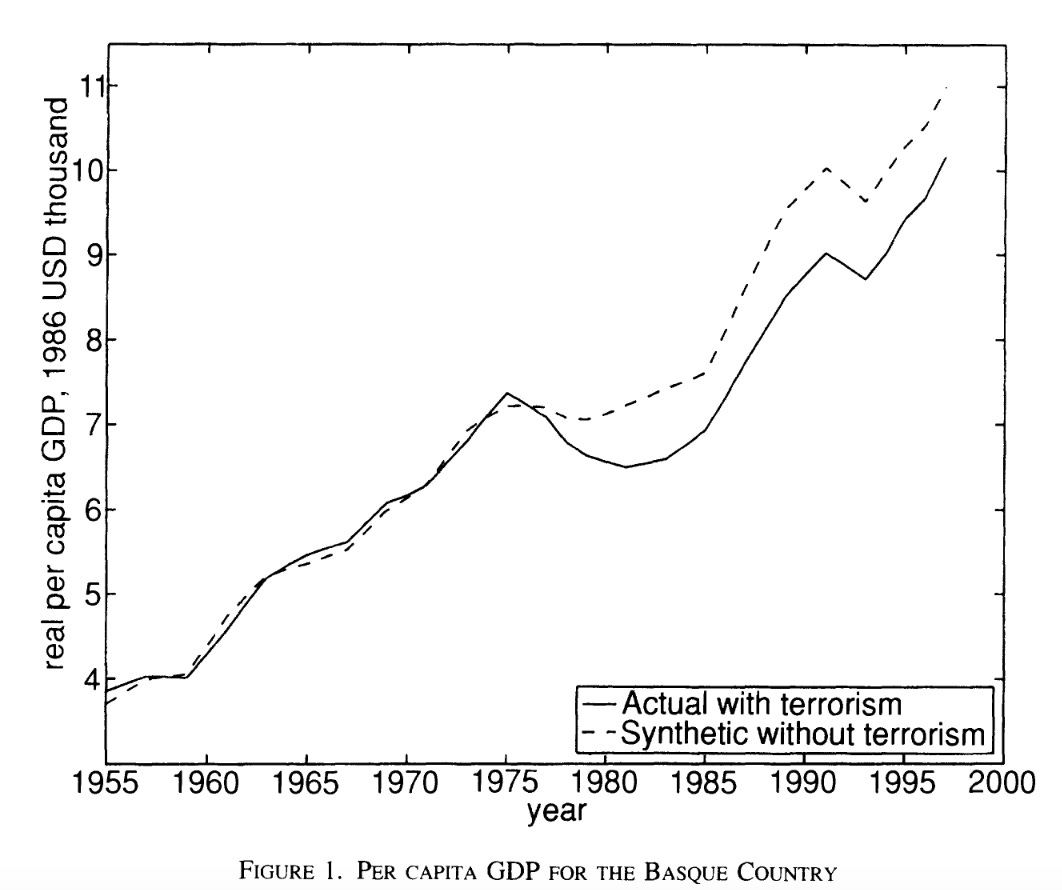
As you can see, they estimate that the ETA’s campaign substantially depressed Basque GDP. Specifically, they find about a 10 percent loss relative to the synthetic counterfactual.

“That’s all very interesting, Charles,” I’m sure you’re thinking, “but why are you telling me this? Wasn’t this supposed to be a post about drug decriminalization?” And the answer is yes, but it’s a post about two different synthetic control estimates of the effects of drug decriminalization. And to understand those, I need you to understand synthetic controls.

I’m telling you about A&G ‘03 because it’s the first example of a now widely used methodology, the synthetic control method. SCM works more or less as I described: you have a bunch of units (states, e.g.), one of which is treated. You want to estimate the effect of the treatment, so you construct a counterfactual by comparing the treated unit to the untreated units on observables—including the outcome—in the pre-treatment period, and constructing a weighted average of the untreated units such that the pre-trends in the outcome match. (You do this using math.)¹ That weighted average is your untreated counterfactual, your “synthetic control.” There are lots of other components, but that’s the basic idea.

SCM is useful in a case where only one jurisdiction has implemented a policy. For example: in November of 2020, Oregon voters passed Measure 110, which decriminalized possession of small quantities of controlled substances throughout the state. Under 110, possession is a violation, subject to a $100 fine (that basically no one pays).² 110’s decriminalization provision came into effect in February of 2021. That same month, the Washington State Supreme Court ruled that the state’s felony drug possession law was unconstitutional because it did not require that the offender be knowingly in possession of the substance. The State Legislature recriminalized possession effective May 2021, but under new more lenient rules. Nonetheless, for a period of three months, there was no statute prohibition possession of drugs in Washington, meaning it also effectively “decriminalized.”³

So we have two jurisdictions that implemented drug decriminalization. What’s the effect of this on overdose deaths? Synthetic controls are a way to answer this question.

But first: what should our assumptions about the effects of decriminalization be? One school of thought is that possession criminalization reduces the supply of and demand for drugs, by making it more costly to carry them and stigmatizing drug use. Another school of thought is that possession criminalization deters people who are addicted from seeking treatment, in turn increasing the duration of addiction and therefore the risk of death. A third school of thought—to which I am always partial—is that policy interventions rarely do anything, so the effect of decriminalization should be assumed to be zero in the absence of evidence otherwise.

What does historical evidence tell us? It’s worth noting that decriminalization isn’t new. Such policies have been pursued in countries as diverse as “Belgium, Estonia, Australia, Mexico, Uruguay, the Netherlands and Portugal.” Possession for consumption has been decriminalized in Spain since the 1970s. European decriminalization was not generally associated with increases in ODs or drug consumption; some argue that Portugal’s decrim helped address their 1990s heroin crisis. America experienced a wave of state-level marijuana decriminalization in the 1970s, which caused a small increase in the prevalence of cannabis use.

There’s only so much we can learn from other decriminalizations, though. That’s partially because they aren’t well-evaluted—historical European OD data are not great—and partially because the particulars of the policy regime matter a lot. As I’ve noted elsewhere, proponents of Oregon’s decriminalization regime often compare it to Portugal. But the Portugese approach depends on a) universal access to treatment and b) the strong “nudge” afforded by its “dissuasion commissions”—Oregon has neither. More generally, I might suggest that European-style decrim depends on a) high therapeutic capacity, b) high interagency and intergovernmental coordination, and c) a willingness to use social pressure through the formal mechanisms of government—all things Americans tend to be very weary of.

But what, actually, has been the effect of Oregon and Washington’s decriminalizations? Two recent papers—Spencer 2023 and Joshi et al. 2023—attempt to answer this question. Specifically, they use the synthetic control method to estimate the effect of both Oregon and Washington’s decriminalizations on overdose deaths. And they come to different conclusions! Why? Let’s find out.

Source: Spencer 2023

Spencer 2023 is by Noah Spencer, an econ PhD student at the University of Toronto. Spencer looks at the effects of decriminalization using data on unintentional drug overdose deaths obtained from the public provisional multiple cause of death database from January 2018 through December 2021. He uses the synthetic control method to estimate the effects of both Oregon and Washington’s decriminalization, using as a donor pool all the other untreated states and DC. In Oregon, he finds an additional 0.39 overdose deaths per 100,000 per month (p = 0.02). In Washington, he finds an additional 0.17 overdose deaths per 100,000 per month (p = 0.02). He does a number of robustness tests: an “in-space” placebo test, in which he re-estimates the model with different states as the treated state, to see if he gets spuriously similar results (he doesn’t); an “in-time” placebo test, in which he re-estimates the model but changes the time of treatment, to see if he gets spuriously similar results (he doesn’t); and a difference-in-difference analysis, which recovers effects of the same magnitude, direction, and significance.

Case closed, right? Nope!

Source: Joshi et al. 2023

Joshi et al. is by a long list of public health people, because public health studies all have ten thousand authors. It looks at the effects of decriminalization using data on all drug poisoning deaths obtained from the restricted use mortality data from January 2018 through March 2022. It uses the synthetic control method to estimate the effects of both Oregon and Washington’s decriminalization, using as a donor pool all the other untreated states and DC. In Oregon, it finds an additional 0.268 overdose deaths per 100,000 per month (p = 0.26). In Washington, it finds an additional 0.112 overdose deaths per 100,000 per month (p = 0.06). Joshi et al. report both of these as nulls, because they are above the p = 0.05 threshold. (I would call p = 0.06 “marginally significant,” but sure.)⁴ They do fewer robustness tests (because they aren’t trying to disconfirm a positive finding), but they do rerun the analysis with a donor pool restricted for fit, and Washington ends up significant (p = 0.04) while Oregon doesn’t.⁵

So in short: both papers report that decrim in both states caused an increase in drug overdose deaths. But in Spencer, the increase is statistically significant; in Joshi et al., it’s not. What explains this difference? And what should we infer from these papers about the effects of decriminalization?

What explains the difference? The two papers use the same methods, but they use data that are subtly but importantly different:

• Spencer uses the public-use data from CDC WONDER. He has to impute some missing cells, because WONDER suppresses state-month cells with deaths fewer than 10. Joshi et al. use the restricted use data files, which can give slightly different numbers, and which do not have suppression. Point Joshi et al.

• Spencer uses data from 2018 through 2021, because those are complete. Joshi et al. add three months of provisional data, through March of 2022. I’m not sure why they select this month, and it seems like a weird choice—what justifies stopping there? They note that less than 1% of deaths in March are pending investigation as of the time of query, so they are unlikely to be off by much. But some of the subsequent months are complete, at least per WONDER. So, weird choices, I think point Spencer.⁶

• Spencer uses CDC WONDER’s annual population estimates to estimate rates; Joshi et al. use the ACS 5-year population figures. I don’t really think this matters either way, but I’m flagging for completeness.

• Death records have two cause of death fields: the “underlying cause of death,” which is the primary cause, and the “multiple cause of death,” which are additional, associated causes. Spencer looks at deaths where the underlying cause was unintentional drug overdoses—ODs can also be suicides, homicides, or undetermined. Joshi et al. look at deaths in which the underlying cause of death is any of these, and the multiple cause of death involved any “drugs, medicaments and biological substances.” Intuitively, I think Spencer is underinclusive. But Joshi et al. also seems overinclusive, because their multiple cause of death codes include poisonings by substances that aren’t conventionally associated with illicit drug overdose. So point neither.

One way to reconcile these results is to say that decrim had a significant impact on unintentional drug overdose deaths, but not on a more expansive category of overdose deaths, and the significance of the effect depends on the period you observe, and possibly which data set you use. But that sounds kind of weird: really, the significance is contingent on these small choices? This is starting to sound like our old friend researcher DFs: if your result is highly sensitive to such small choices, be wary of it!

Another way to reconcile these results would be to try to zero in on some agreeable reconciliation of the discrepancies. For example, the above chart depicts an SCM analysis I ran (code here) using the public use (CDC WONDER) data, including its population estimates as denominators, covering Jan. 2018 - Mar. 2022 (I just count months as “period”), using drug overdose underlying causes and multiple causes involving synthetic opioids (T40.4), heroin (T40.1), and other opioids (T40.2). I estimate Oregon added 0.734 opioid OD deaths per 100,000 per month (p = 0.104), and Washington added 0.963 opioid OD deaths per 100,000 per month (p = 0.0204).

Here, Oregon is probably not significant, and Washington is definitely significant. On the other hand, the pre-trend fit isn’t great, and this is something I did in R in half an hour, not a peer-reviewed publication (so please do not cite it). What is more, the analysis is subject to exactly the same criticisms about data selection and reseacher DFs. It’s also pretty sensitive: if I use full provisional data through the end of 2022, both Oregon and Washington are significant (p = 0.0204). On the other hand, due to an error in coding I initially ran it imputing missing values between 1 and 8, and that ended up with Oregon as significant too. Goes to show how touchy it is.

Ideally, you’d rerun the analysis with a bunch of different inputs, and see what the balance of the outcomes looks like. (Also, ideally, you’d do it with more pre and post data.) I’m not going to do that, mostly for want of time, but if one of the authors wants to, they should!

Instead, I’m going to zoom out and ask: how should we interpret these two papers? Should we conclude that decrim increased OD deaths, or had no effect? I think there is a parsimonious case for both positions, and I’m going to lay them both out.

The case for no effect is, basically, that we should by default be skeptical of interventions having an effect, particularly when findings are highly sensitive to seemingly innocuous choices. If adding three months’ worth of data, choosing a slightly different definition of drug OD, and using a different data set changes the significance of our findings, that should cause us to be wary of the idea that we’ve really found something. If your effect is real, it should show up in a variety of different specifications and be apparent in a variety of different tests. And I don’t think we’ve met that threshold here.

The case for an effect is that the difference between the two papers comes down not to the magnitude or direction of the effects—which are similar across papers and specifications—but statistical significance. And the use of statistical significance is, well, highly controversial! And it’s weird specifically with SCM.

Why? Very briefly: statistical significance is often measured with reference to p-values, with the somewhat arbitrary assumption that p < 0.05 means significance. What’s a p-value? In many (although not all) analyses, a p-value is a measure of how likely it is that you would get a result as extreme as your estimate, given that the true value is zero.⁷ To determine it, you estimate the distribution of possible results from your sampling process, given that the true value is zero, then compare your estimate to this distribution.⁸

How do you do this in a synthetic control? Basically, you do the in-space placebo test: you rerun the synthetic control, but pretending the untreated units are the treated units. You then compare the treated unit’s outcome⁹ to the distribution generated by this process, rank them, and estimate the p-value as the rank of the treated unit’s outcome over the total number of outcomes in your distribution. So e.g. Spencer consistently finds that Washington and Oregon have the most extreme outcomes, so the p-values are rank 1/50 units = 0.02. Joshi et al. find that Oregon ranks 13th out of 50 units, so p = 0.26, while Washington is 3rd out of 50 units, so p = 0.06.¹⁰

This all makes some sense to me, but also feels like a weird way to test statistical significance. Does it make sense to me to say that we can’t rule out (fail to reject) the possibility that Oregon and Washington might have experienced these deviations by chance because other states experienced deviations just as or more extreme? Sure. But we don’t usually use a handful of untreated units to generate the null distribution for hypothesis testing, and I’m not sure how I feel about doing it here. And in other contexts, if you told me that you had a positive but insignificant effect in an N = 50 sample, I would tell you you might need more power to really say anything. I might call your finding “suggestive.” I wouldn’t necessarily conclude that there was no effect, especially if other specifications reached significance.

Anyway, you can decide which view you find more persuasive. But I want to leave by emphasizing another, important takeaway: from neither of these studies can you infer that decriminalization reduced drug overdose deaths.

Here I want to editorialize for a minute. The purpose of the Drug Addiction Treatment and Recovery Act—the full title of Oregon’s decrim measure—was the expansion of treatment in the state in the union with the greatest unmet treatment need. Pro-110 ads framed it as the alternative to the failed approach of criminalization. Joshi et al. cite a great deal of literature calling for drug decriminalization as a necessary public health intervention, because it will prevent overdoses and save lives.

In the American context, the best evidence we have so far is that this is simply false. Maybe it will change—a lot depends, as I’ve said, on the regime. But it is extremely telling in my view that the Drug Policy Alliance—which spent $5 million on 110 and —is now trumpeting Joshi et al. as proof that decriminalization didn’t make things worse.

Let’s pretend that we can say for sure that that’s true. Is that the best we can ask for?

1. If you want some of the nitty gritty, I used the chapter on SCM in Scott Cunningham’s Causal Inference: The Mixtape as a reference in writing this post.

2. I reported on 110 extensively for City Journal, which I encourage you to check out here.

3. Obviously, making something an administrative violation vs. simply not having a rule against it are two different actions, with two different consequences. This is one of the reasons the language of “decriminalization” is confusing. Insofar as there was no formal prohibition against possession, I think it is fair to say that possession was “legalized” by the Washington Supreme Court, whereas “decriminalized” or “depenalized” is more appropriate for Oregon. But, given that neither regime actually created any form of legal regime for sale or distribution of drugs, I’m comfortable just calling them both “decriminalized” for now.

4. Honestly, I think it’s nonsensical to read these papers and not conclude the Blake decision increased OD deaths. Across all specifications, the value is positive and p < 0.10. Joshi et al. are abusing a technicality here.

5. They also do some “weighted controlled interrupted time series analyses,” which I think might be public health speak for diff-in-diff, but I don’t know and can’t access the supplements because they’re behind the paywall.

6. Also, neither paper uses pre-2018 data. Why? It’s public! It’s comparable back to 1999! Length of pre-period matters for SCM! I think this is just laziness on everyone’s part, to be quite honest.

7. “That’s not always what a p-value is!” Yes, I know. I don’t want to explain hypothesis testing from the ground up. I’m trying to make a point.

8. Again, yes, I know, this isn’t precisely correct, I’m going somewhere.

9. The relevant statistic is the ratio of the mean squared prediction error before and after the intervention, if you care.

10. There are apparently other ways to get p-values for SCMs—see here, e.g.—but neither of our authors does them and the package I used doesn’t support them.